This is part five of a series on the Random Oracle Model. See here for the previous posts: Part 1: An introduction Part 2: The ROM formalized, a scheme and a proof sketch Part 3: How we abuse the ROM to make our security proofs work Part 4: Some more examples of where the ROM […]
Category Archives: Uncategorized
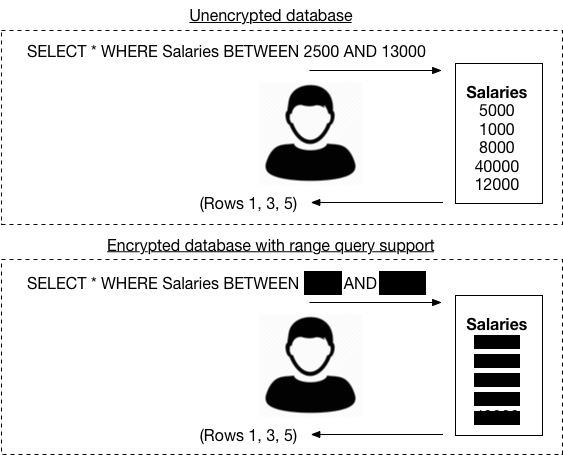
Attack of the week: searchable encryption and the ever-expanding leakage function — A Few Thoughts on Cryptographic Engineering
A few days ago I had the pleasure of hosting Kenny Paterson, who braved snow and historic cold (by Baltimore standards) to come talk to us about encrypted databases. Kenny’s newest result is with first authors Paul Grubbs, Marie-Sarah Lacharité and Brice Minaud (let’s call it GLMP). It isn’t so much about building encrypted databases, as it […]
DUKPT Explained with examples
Derived Unique Key Per Transaction (DUKPT) process that’s described in Annex A of ANS X9.24-2004.
It’s generally considered to be complex, but I’ve simplified it slightly with the help of online resources.
Key Management
Here’s a basic outline of the technique:
- You’re given a Base Derivation Key (BDK), which you assign to a swiper (note that the same BDK can be assigned to multiple swipers).
- You’ll use the BDK along with the device’s own unique Key Serial Number (KSN) to generate an Initial PIN Encryption Key (IPEK) for the device.
- You’ll assign this IPEK to a swiper, which uses it to irreversibly generate a list of future keys, which it’ll use to encrypt its messages.
- The swiper’s KSN is used along with one of its future keys to encrypt a message, and after each swipe it’ll increment the value of its KSN.
- Whenever a swiper takes a card it formats the card’s information into a series of tracks, each track having a particular set of information (e.g. card number, holder’s name, expiration date).
- The swiper usually encrypts these tracks using one of its generated future keys (called the “Session Key”) along with its current KSN. It’ll then increment the value of its KSN and discard the future key it used.
- At this point you’ll probably have an encrypted track along with the KSN the swiper used to encrypt it.
- It’s your responsibility to determine what BDK was used to initialize this device, and from there you’ll use the BDK and KSN to rederive the IPEK, which is used to rederive the Session Key, which is finally used to decrypt the message.
There’s a lot of technical information to be said about key management, but this isn’t the place for that. In some cases your provider/manufacturer (e.g. MagTek) will supply you with swipers that need to be initialized with an IPEK, and your supplier will usually have a manual that walks you through that process. If you’re doing encryption/decryption through a third party who also supplies swipers, they may have already loaded the devices with that information; what’s more is they may not even given you the BDK that belongs to your device in order to reduce the risk of security threats.
Note: Key management is beyond the scope of this explanation. Whatever you do with your keys, just make sure it’s secure.
One methodology I’ve seen that’ll allow you to associate a particular KSN to a BDK is to take the current KSN you’ve been given, mask it to retrieve the Initial Key Serial Number (IKSN), and look up the BDK in a table that maps IKSNs to BDKs:
Example:
ksn = FFFF9876543210E00008
iksn = ksn & FFFFFFFFFFFFFFE00000 // FFFF9876543210E00000
You’d then have a table that looks like:
| IKSN | BDK |
|---|---|
| 0xFFFF9876543210E00000 | 0123456789ABCDEFFEDCBA9876543210 |
| … | … |
From which you could easily grab the BDK 0123456789ABCDEFFEDCBA9876543210.
Algorithm
Note: Assume that all numeric values are hexadecimal numbers, or the representation of a sequence of bytes as a hexadecimal number.
The following are the BDK, KSN, and encrypted track message (cryptogram) we’ve been given:
bdk = 0123456789ABCDEFFEDCBA9876543210
ksn = FFFF9876543210E00008
cryptogram = C25C1D1197D31CAA87285D59A892047426D9182EC11353C051ADD6D0F072A6CB3436560B3071FC1FD11D9F7E74886742D9BEE0CFD1EA1064C213BB55278B2F12
Here’s an example of the unencrypted track 1 data (cryptogram above), and below that is its value in hex; this is what we’ll get after successfully decrypting the cryptogram:
%B5452300551227189^HOGAN/PAUL ^08043210000000725000000?
2542353435323330303535313232373138395E484F47414E2F5041554C2020202020205E30383034333231303030303030303732353030303030303F00000000
Note: As you’re probably already aware, this algorithm is best described using big numbers, which can’t be represented as literals in some programming languages (like Java or C#). However, many languages have classes that allow you to represent big numbers in other ways (e.g., java.math.BigInteger, System.Numerics.BigInteger). It’s your job to adapt this algorithm so that it can be represented in your language of choice. Two small problems I encountered were ensuring the correct endianness and signedness were being used (this algorithm requires the byte order to be big endian and that unsigned integers are used). I made a utility class called BigInt to do this for me.
First, let’s define a few standard functions:
- DES and Triple DES refer to their respective cryptographic algorithms. Most programming languages have access to some implementation of these ciphers either through OpenSSL or Bouncy Castle. These ciphers are initialized with a zeroed out IV of 8 bytes, they’re zero-padded, and use Cipher-Block Chaining (CBC). Let’s define the signatures for these standard functions that’ll be used throughout this algorithm:
DesEncrypt(key, message) -> returns cryptogramDesDecrypt(key, cryptogram) -> returns messageTripleDesEncrypt(key, message) -> returns cryptogramTripleDesDecrypt(key, cryptogram) -> returns message
First we must create the IPEK given then KSN and BDK:
CreateIpek(ksn, bdk) {
return TripleDesEncrypt(bdk, (ksn & KsnMask) >> 16) << 64
| TripleDesEncrypt(bdk ^ KeyMask, (ksn & KsnMask) >> 16)
}
Now we can get the IPEK:
ipek = CreateIpek(ksn, bdk)
= CreateIpek(FFFF9876543210E00008, 0123456789ABCDEFFEDCBA9876543210)
= 6AC292FAA1315B4D858AB3A3D7D5933A
After that we need a way to get the Session Key (this one is more complicated):
CreateSessionKey(ipek, ksn) {
return DeriveKey(ipek, ksn) ^ FF00000000000000FF
}
The DeriveKey method finds the IKSN and generates session keys until it gets to the one that corresponds to the current KSN. We define this method as:
DeriveKey(ipek, ksn) {
ksnReg = ksn & FFFFFFFFFFE00000
curKey = ipek
for (shiftReg = 0x100000; shiftReg > 0; shiftReg >>= 1)
if ((shiftReg & ksn & 1FFFFF) > 0)
curKey = GenerateKey(curKey, ksnReg |= shiftReg)
return curKey
}
Where the GenerateKey method looks like:
GenerateKey(key, ksn) {
return EncryptRegister(key ^ KeyMask, ksn) << 64
| EncryptRegister(key, ksn)
}
And EncryptRegister looks like:
EncryptRegister(key, reg) {
return (key & FFFFFFFFFFFFFFFF) ^ DesEncrypt((key & FFFFFFFFFFFFFFFF0000000000000000) >> 64,
key & FFFFFFFFFFFFFFFF ^ reg)
}
Then you can generate the Session Key given the IPEK and KSN:
key = CreateSessionKey(ipek, ksn)
= CreateSessionKey(6AC292FAA1315B4D858AB3A3D7D5933A, FFFF9876543210E00008)
= 27F66D5244FF621EAA6F6120EDEB427F
Which can be used to decrypt the cryptogram:
message = TripleDesDecrypt(key, cryptogram)
= TripleDesDecrypt(27F66D5244FF621EAA6F6120EDEB427F, C25C1D1197D31CAA87285D59A892047426D9182EC11353C051ADD6D0F072A6CB3436560B3071FC1FD11D9F7E74886742D9BEE0CFD1EA1064C213BB55278B2F12)
= 2542353435323330303535313232373138395E484F47414E2F5041554C2020202020205E30383034333231303030303030303732353030303030303F00000000
= %B5452300551227189^HOGAN/PAUL ^08043210000000725000000?
That’s it, you’re done!
Implementing AS2805 Part 6 Host to Host Encryption using a Thales 9000 and Python
Introduction
The AS2805.6 Standard specifies communication security between two nodes during a financial transaction. These nodes needs to have a specific set of encryption algorithms, and needs to follow a specific process.
The specification is not very clear on what exactly needs to happen, so I intend to clarify the exact steps, with the HSM functions. Now in order to do this I will assume you have a Thales 9000 HSM, as well as you need to know how to properly operate it. All commands defined are in the 1270A547-015 Australian Standards LIC003 v2.3a.pdf Manual provided by Thales when purchasing the device.
Source Code
a Copy of this Manual can be found here [Thales 9000 Australian Standards LIC003 v2.3a]
a Copy of my AS2805 parser is located here
a Copy of my Thales commands class is located here
a Full version of a AS2805 Interchange Node is located here
KEK Process (Level 1)
For this process:
- you need to go to your HSM and generate 2 Clear components, you then need to form a KEKs key from these components. This can be done using the UI of the HSM manger, or with the FK console command.
- Store the KEKs formed from the clear components in your switch database.
- Your connecting node / host will then provide you with a set of clear components, you need to generate a key again, but in this case a KEKr
- You need to provide you host with your key components you generated in Step 1,so they can generate their corresponding KEKs.
Now you have a KEKr and a KEKs in your database as well as your host read, for Level2
Session and MAC key Initialisation (Level 2)
This Level has 2 separate steps, the first step (Logon) validating the KEKr and KEKs so that both nodes know that the correct keys are being used. The second step (Key Exchange) is to create temporary keys that are changed every 60 minutes or 256 transactions.
Logon Process
During the logon process your HSM will need to generate 2 things:
- a Random Number (RN)
- an Inverted Random Number (~RN)
These numbers will be returned encrypted under the KEKr and KEKs, and you will need to validate them, this is also called end of proof point validation.
The Logon process is a 2 step process outlined in the image below.
Step 1
When you connect to your host you will receive a logon request, bit number 48 will be populated with a KRs from the host that you will need to validate with your KEKr.
Generating a KEKr Validation Response you would need your KRs received in this request, and you KEKr that you generated from your host components.
E2 Command Definition: To receive a random key (KRs) encrypted under a variant of a double length Key Encrypting Key (KEKr), compute from KRs another value, denoted KRr and encrypt it under another variant of the KEKr
Your HSM command will look as follows: >HEADE2{KEKr}{KRs} and you output will generate a KEKr. Your response to the host will need to include this value in bit number 48.
Step 2
You now need to send the host a logon request with bit 48 set with your KRs
E0 Command Definition:To generate a random key (KRs) and encrypt it with a variant of a double length Key Encrypting Key (KEKs). In addition, KRs is inverted (to form KRr) and the result encrypted with another variant of the KEKs.
Your HSM command will look as follows: >HEADE0{KEKs} and the output will generate a KRs. Your host will validate this request, and return with a response.
Once both steps are complete, both you and the host has been validated that you are using the same keys.
An Example of this process is outlined below in Python:
def __signon__Part1__(self):
self.log.info("====Sign-On Process Started ====")
self.__setState('signing_on')
cur = self.con_switch.cursor(MySQLdb.cursors.DictCursor)
try:
self.log.info("Waiting for 0800 Request")
self.s.settimeout(20.0)
length_indicator = self.s.recv(2)
if length_indicator == '':
self.log.critical('Received a blank length indicator from switch... might be a disconnect')
self.__setState("blank_response")
else:
size = struct.unpack('!H', length_indicator)[0]
payload = self.s.recv(size)
payload = ByteUtils.ByteToHex(payload)
d = datetime.now()
self.log.info(" Getting Sign-On Request 0800 = [%s]" % payload)
if payload == '':
self.log.critical('Received a blank response from switch... might be a disconnect')
self.__setState("blank_response")
else:
iso_ans = AS2805(debug=False)
iso_ans.setIsoContent(payload)
self.__storeISOMessage(iso_ans, {"date_time_received": d.strftime("%Y-%m-%d %H:%M:%S")})
if iso_ans.getMTI() == '0800':
if iso_ans.getBit(70) == '001':
#log.info("Logon Started with KEKr = %s, KEKs = %s" % ( self.KEKr, self.KEKs))
KRs = iso_ans.getBit(48)
#log.info("KRs %s Received from Host" % (KRs))
#print "Generating a E0 Command with KEKr=%s, and KRs=%s" % (self.KEKr, KRs)
self.ValidationResponse = KeyGenerator.Generate_KEKr_Validation_Response(KEKr=self.KEKr, KRs=KRs)
#print self.ValidationResponse
if self.ValidationResponse["ErrorCode"] == '00':
#log.info("KRs Validation Response %s generated" % (self.ValidationResponse["KRr"]))
d = datetime.now()
iso_resp = AS2805(debug=False)
iso_resp.setMTI('0810')
iso_resp.setBit(7, d.strftime("%m%d%H%M%S"))
iso_resp.setBit(11, iso_ans.getBit(11))
iso_resp.setBit(33, self.Switch_IIN)
iso_resp.setBit(39, '303')
iso_resp.setBit(48, self.ValidationResponse["KRr"])
iso_resp.setBit(70, '0001')
iso_resp.setBit(100, self.Switch_IIN)
iso_send = iso_resp.getNetworkISO()
iso_send_hex = ByteUtils.HexToByte(iso_send[2:])
self.log.info("Sending Sign-On Response 0810 [%s]" % ReadableAscii(iso_send))
self.__send_message(iso_send_hex)
self.__storeISOMessage(iso_resp, {"date_time_sent": d.strftime("%Y-%m-%d %H:%M:%S")})
self.__setState('signed_on')
else:
self.log.error("0810 KRr Response Code = %s, Login Failed" % (self.ValidationResponse["ErrorCode"],))
#TODO: Send Decline to the Partner
else:
self.log.error("Could not login with 0810")
except InvalidAS2805, ii:
self.log.error(ii)
except socket.error as e:
pass
self.log.debug("nothing from host [%s]" % (e))
except:
#self.__signoff()
self.log.exception("signon_failed")
self.__setState("singon_failed")
finally:
cur.close()
def __signon_Part2__(self):
try:
self.s.settimeout(20.0)
self.ValidationRequest = KeyGenerator.Generate_KEKs_Validation_Request(KEKs=self.KEKs)
d = datetime.now()
iso_resp = AS2805(debug=False)
iso_resp.setMTI('0800')
iso_resp.setBit(7, d.strftime("%m%d%H%M%S"))
iso_resp.setBit(11, self.__getNextStanNo())
iso_resp.setBit(33, self.HostIIN)
iso_resp.setBit(48, self.ValidationRequest["KRs"])
iso_resp.setBit(70, '001')
iso_resp.setBit(100, self.HostIIN)
iso_send = iso_resp.getNetworkISO()
iso_send_hex = ByteUtils.HexToByte(iso_send[2:])
self.log.info("Sending Sign-On Request 0800 [%s]" % ReadableAscii(iso_send))
self.__send_message(iso_send_hex)
self.__storeISOMessage(iso_resp, {"date_time_sent": d.strftime("%Y-%m-%d %H:%M:%S")})
self.log.info("Waiting for 0810 Response")
a = self.s.recv(8192)
payload = ByteUtils.ByteToHex(a[2:])
d = datetime.now()
self.log.info(" Getting Sign-On Response 0810 = [%s]" % payload)
iso_ans = AS2805(debug=False)
iso_ans.setIsoContent(payload)
self.log.debug(iso_ans.dumpFields())
self.__storeISOMessage(iso_ans, {"date_time_received": d.strftime("%Y-%m-%d %H:%M:%S")})
if iso_ans.getBit(39) == '3030':
self.log.info("====Sign-On Sequence Completed Successfully====")
self.__setState("signed_on_dual")
else:
#self.__signoff()
self.log.error("Could not login with 0800")
self.__setState("singon_failed")
except InvalidAS2805, ii:
self.log.info(ii)
except socket.error as e:
self.log.info("nothing from host [%s]" % (e))
except:
#self.__signoff()
self.log.exception("signon_failed")
self.__setState("singon_failed")
Key Exchange (Level 2)
In the Key Exchange process, you will generate session keys for your node as well as MAC keys. Now when generating these keys, you need to remember that they need to be the same type as you partner node. (simply ask your processor for a trace if you want to confirm)
So right after a successful logon, you would need to wait for a key exchange request, (0820 with field 30 as 303) this key exchange request will have a ZAK and a ZPK in field 48, these are encrypted under the KEKr generated on your host from their components. You would need to translate these keys using your KEKr under your LMK and generate check values for verification.
The command will look like follows: >HEADOK{KEKr}21H{ZPK}1H{ZAK}0H11111111111111111111111111111111
These keys are known as your: RECEIVE KEYS
Where the KEKr is the KEKr generated from your components, ZPK and ZAK is the ZPK and ZAK received. This will output the following:
def Translate_a_Set_of_Zone_Keys(KEKr, ZPK, ZAK, ZEK):
response = KeyClass.execute_Translate_a_Set_of_Zone_Keys(KEKr, ZPK, ZAK, ZEK)
#print response
TranslatedZoneKeys = {}
TranslatedZoneKeys["Header"] = response[2:6]
TranslatedZoneKeys["ResponseCode"] = response[6:8]
TranslatedZoneKeys["ErrorCode"] = response[8:10]
if TranslatedZoneKeys["ErrorCode"] == '00':
TranslatedZoneKeys["KCV Processing Flag"] = response[10:11]
TranslatedZoneKeys["ZPK(LMK)"] = response[11:44]
TranslatedZoneKeys["ZPK Check Value"] = response[44:50]
TranslatedZoneKeys["ZAK(LMK)"] = response[50:83]
TranslatedZoneKeys["ZAK Check Value"] = response[83:89]
TranslatedZoneKeys["ZEK(LMK)"] = response[89:122]
TranslatedZoneKeys["ZEK Check Value"] = response[122:128]
return TranslatedZoneKeys
In other words, you need to generate the same keys, but under your LMK and store them in your key database
Now whenever you get a request from your host with a mac you can validate the mac using the ZAK(LMK), and when you get encrypted values from your host you can translate the values using the ZPK(LMK)
So, when you respond to the key exchange process you put the check values in field 40. Your host will validate the check values, and then wait for you to send a request using your KEKs.
Here is an implementation using Python:
def __key_exchange_listen(self):
self.log.info("===== Key Exchange process Started =======")
self.s.settimeout(20.0)
length_indicator = self.s.recv(2)
if length_indicator == '':
self.log.critical('Received a blank length indicator from switch... might be a disconnect')
self.__setState("blank_response")
else:
size = struct.unpack('!H', length_indicator)[0]
payload = self.s.recv(size)
payload = ByteUtils.ByteToHex(payload)
d = datetime.now()
self.log.info(" Receiving Key Exchange Request = [%s]" % payload)
if payload == '':
self.log.critical('Received a blank response from switch... might be a disconnect')
self.__setState("blank_response")
else:
iso_ans = AS2805(debug=False)
iso_ans.setIsoContent("%s" % (payload))
self.log.debug(iso_ans.dumpFields())
self.__storeISOMessage(iso_ans, {"date_time_received": d.strftime("%Y-%m-%d %H:%M:%S")})
if iso_ans.getMTI() == '0820' and iso_ans.getBit(70) == '0101':
Value = iso_ans.getBit(48)
self.ZAK = Value[:32]
self.ZPK = Value[32:]
self.node_number = iso_ans.getBit(53)
log.info("Recieve Keys under ZMK : ZAK= %s, ZPK = %s" % (self.ZAK, self.ZPK ))
self.ZoneKeySet2 = KeyGenerator.Translate_a_Set_of_Zone_Keys(self.KEKr,ZPK=self.ZPK, ZAK=self.ZAK, ZEK='11111111111111111111111111111111')
cur = self.con_switch.cursor(MySQLdb.cursors.DictCursor)
sql = """UPDATE sessions_as2805 set
ZPK_LMK = '%s',
ZPK_ZMK = '%s',
ZPK_Check ='%s',
ZAK_LMK = '%s' ,
ZAK_ZMK = '%s',
ZAK_Check = '%s',
ZEK_LMK = '%s',
ZEK_Check = '%s',
keyset_number = '%s'
WHERE host_id = '%s' and keyset_description = 'Recieve' """ %\
(
self.ZoneKeySet2["ZPK(LMK)"],
self.ZPK,
self.ZoneKeySet2["ZPK Check Value"],
self.ZoneKeySet2["ZAK(LMK)"],
self.ZAK,
self.ZoneKeySet2["ZAK Check Value"],
self.ZoneKeySet2["ZEK(LMK)"],
self.ZoneKeySet2["ZEK Check Value"],
self.node_number,
self.host_id)
log.info("Recieve Keys under LMK : ZAK= %s, ZAK Check Value: %s ZPK = %s, ZPK Check Value: %s" % (self.ZoneKeySet2["ZAK(LMK)"], self.ZoneKeySet2["ZAK Check Value"], self.ZoneKeySet2["ZPK(LMK)"], self.ZoneKeySet2["ZPK Check Value"]))
cur.execute(sql)
self.log.debug("Records=%s" % (cur.rowcount,))
iso_req = AS2805(debug=False)
iso_req.setMTI('0830')
iso_req.setBit(7, iso_ans.getBit(7))
iso_req.setBit(11, iso_ans.getBit(11))
iso_req.setBit(33, iso_ans.getBit(33))
iso_req.setBit(39, '303')
iso_req.setBit(48, self.ZoneKeySet2["ZAK Check Value"] + self.ZoneKeySet2["ZPK Check Value"])
iso_req.setBit(53, iso_ans.getBit(53))
iso_req.setBit(70, iso_ans.getBit(70))
iso_req.setBit(100, iso_ans.getBit(100))
self.__storeISOMessage(iso_req, {"date_time_sent": d.strftime("%Y-%m-%d %H:%M:%S")})
try:
iso_send = iso_req.getNetworkISO()
iso_send_hex = ByteUtils.HexToByte(iso_send[2:])
self.log.debug(iso_req.dumpFields())
self.log.info("Sending Key Exchange Response = [%s]" % ReadableAscii(iso_send))
self.__send_message(iso_send_hex)
self.node_number = iso_ans.getBit(53)
except:
self.log.exception("key_exchange_failed")
self.__setState('key_exchange_failed')
finally:
cur.close()
These Keys are known as your SEND KEYS
So when you send a key exchange request you would need to generate a set of zone keys, this command on your HSM would look like this;
>HEADOI{KEKs};HU;1
Where the KEKs is the KEKs that you generated from your components, and your output will be the following:
def Generate_a_Set_of_Zone_Keys(KEKs):
response = KeyClass.execute_get_a_Set_of_Zone_Keys(KEKs)
#print response
ZoneKeys = {}
ZoneKeys["Header"] = response[2:6]
ZoneKeys["ResponseCode"] = response[6:8]
ZoneKeys["ErrorCode"] = response[8:10]
if ZoneKeys["ErrorCode"] == '00':
ZoneKeys["ZPK(LMK)"] = response[10:43]
ZoneKeys["ZPK(ZMK)"] = response[43:76]
ZoneKeys["ZPK Check Value"] = response[76:82]
ZoneKeys["ZAK(LMK)"] = response[82:115]
ZoneKeys["ZAK(ZMK)"] = response[115:148]
ZoneKeys["ZAK Check Value"] = response[148:154]
ZoneKeys["ZEK(LMK)"] = response[154:187]
ZoneKeys["ZEK(ZMK)"] = response[187:220]
ZoneKeys["ZEK Check Value"] = response[220:226]
return ZoneKeys
Now when sending your 0820 request, you need to set field 40 as ZAK(ZMK) + ZPK(ZMK). Your host will do a Validation request (same as you did in step 1) and send you the check values. you need to compare this to the check values generated by your OI command, and if they match then you have successfully exchanged keys.
Below is an implementation using Python:
def __keyExchange__(self):
self.__setState("key_exchange")
self.__key_exchange_listen()
cur = self.con_switch.cursor(MySQLdb.cursors.DictCursor)
d = datetime.now()
self.ZoneKeySet1 = {}
self.ZoneKeySet2 = {}
self.ZoneKeySet1 = KeyGenerator.Generate_a_Set_of_Zone_Keys(self.KEKs)
iso_req = AS2805(debug=False)
iso_req.setMTI('0820')
iso_req.setBit(7, d.strftime("%m%d%H%M%S"))
iso_req.setBit(11, self.__getNextStan())
iso_req.setBit(33, self.HostIIN)
iso_req.setBit(48, self.ZoneKeySet1["ZAK(ZMK)"][1:] + self.ZoneKeySet1["ZPK(ZMK)"][1:])
iso_req.setBit(53, self.node_number)
iso_req.setBit(70, '101')
iso_req.setBit(100, self.SwitchLink_IIN)
self.__storeISOMessage(iso_req, {"date_time_sent": d.strftime("%Y-%m-%d %H:%M:%S")})
log.info("Send Keys under LMK : ZAK= %s, ZAK Check Value: %s ZPK = %s, ZPK Check Value: %s" % (self.ZoneKeySet1["ZAK(LMK)"], self.ZoneKeySet1["ZAK Check Value"], self.ZoneKeySet1["ZPK(LMK)"], self.ZoneKeySet1["ZPK Check Value"]))
try:
# send the Send Keys
iso_send = iso_req.getNetworkISO()
iso_send_hex = ByteUtils.HexToByte(iso_send[2:])
self.log.debug(iso_req.dumpFields())
self.log.info("Sending Key Exchange Request = [%s]" % ReadableAscii(iso_send))
self.__send_message(iso_send_hex)
self.s.settimeout(20.0)
length_indicator = self.s.recv(2)
if length_indicator == '':
self.log.critical('Received a blank length indicator from switch... might be a disconnect')
self.__setState("blank_response")
else:
size = struct.unpack('!H', length_indicator)[0]
payload = self.s.recv(size)
payload = ByteUtils.ByteToHex(payload)
d = datetime.now()
self.log.info(" Receiving Key Exchange Response = [%s]" % payload)
if payload == '':
self.log.critical('Received a blank response from switch... might be a disconnect')
self.__setState("blank_response")
else:
iso_ans = AS2805(debug=False)
iso_ans.setIsoContent(payload)
self.log.debug(iso_ans.dumpFields())
self.__storeISOMessage(iso_ans, {"date_time_received": d.strftime("%Y-%m-%d %H:%M:%S")})
if iso_ans.getMTI() == '0830':
if iso_ans.getBit(39) == '3030':
Value = iso_ans.getBit(48)
self.KMACs_KVC = Value[:6]
self.KPEs_KVC = Value[6:]
#self.log.info("KMACs_KVC = %s, KPEs_KVC = %s" % (self.KMACs_KVC, self.KPEs_KVC))
if self.KMACs_KVC == self.ZoneKeySet1["ZAK Check Value"] and self.KPEs_KVC == self.ZoneKeySet1["ZPK Check Value"]:
self.log.info("0820 Key Exchange successful: Check Values Match, ZAK Check Value= %s , ZPK Check Value = %s" % (self.ZoneKeySet1["ZAK Check Value"], self.ZoneKeySet1["ZPK Check Value"]))
sql = """UPDATE sessions_as2805
SET
ZPK_LMK = '%s',
ZPK_ZMK = '%s',
ZPK_Check= '%s' ,
ZAK_LMK= '%s',
ZAK_ZMK = '%s',
ZAK_Check ='%s',
ZEK_LMK = '%s' ,
ZEK_ZMK = '%s',
ZEK_Check = '%s',
keyset_number = '%s'
WHERE host_id = '%s' and keyset_description = 'Send' """%\
( self.ZoneKeySet1["ZPK(LMK)"],
self.ZoneKeySet1["ZPK(ZMK)"],
self.ZoneKeySet1["ZPK Check Value"],
self.ZoneKeySet1["ZAK(LMK)"],
self.ZoneKeySet1["ZAK(ZMK)"],
self.ZoneKeySet1["ZAK Check Value"],
self.ZoneKeySet1["ZEK(LMK)"],
self.ZoneKeySet1["ZEK(ZMK)"],
self.ZoneKeySet1["ZEK Check Value"],
self.node_number,
self.host_id)
cur.execute(sql)
self.log.debug("Records=%s" % (cur.rowcount,))
self.__setState("key_exchanged")
self.__setState('session_key_ok')
self.log.info("==== Key Exchange Sequence Completed Successfully====")
self.last_key_exchange = datetime.now()
else:
self.log.error("Generate_a_Set_of_Zone_Keys: KVC Check Failed!!")
else:
self.log.error("0820 Response Code = %s, Key Exchange Failed" % (iso_ans.getBit(39)))
except InvalidAS2805, ii:
self.log.error(ii)
self.s.close()
self.s = None
self.__setState("session_key_fail")
except:
self.log.exception("key_exchange_failed")
self.__setState('key_exchange_failed')
Now that keys have successfully been exchanged, you can start submitting transactions.
When sending transactions encrypt data (pin / field) Send Keys, and when receiving data translate / decrypt using your receive keys, Generate MAC using Send MAC and Verify using Receive MAC.
- TAK – Your key to generate and verify MACs
- TEK – Your key to encrypt data and decrypt / translate
This concludes the implementation of Node to Node interfaces using AS2805 Standards.
Easy as Pie!
Typical Cryptography in AS2805 Explained
Key Management conforms to AS 2805 part 6.1.
KEK Establishment
Each interchange node contains an Interchange Send Key Encrypting Key (KEKs) and an Interchange Receive Key Encrypting Key (KEKr). The Interchange Send KEK is the same key as the Interchange Receive KEK in the partnering node, similarly the Interchange Receive KEK is the same as the Interchange Send KEK in the partnering node.
The Interchange Key Encrypting Keys are used to encipher and decipher the session keys when they are transmitted between the nodes and in the proof of end points process.
Interchange Key Encrypting Keys is statistically unique and shall be changed, at a minimum, once every two years.
| Node A | Node B | ||
| KEKs | = | KEKr | |
| KEkr | = | KEKs | |
Session Keys
Each node keeps four sets of session keys, two send sets and two receive sets.
Each set of session keys consists of two keys, MAC Key, PIN Protect Key. Each session key is 128-bits long and stored in a secure manner.
The send session key sets are generated by the sending node and numbered “1” or “2”. The send session key sets are then forwarded to the receiving node to be used as the receive session key sets.
The receive session key sets are received in a 0820 Network Management Advice message with bit ‘070’ equal to 101 from the sending node. The set number of either “1” or “2” contained in bit 53 indicates the receive session key set used by the receiving node to verify the MAC, decipher the data and translate or verify the PIN.
One set of send session keys is used at a time and all Transactions sent from the sending node will generate the MAC and encipher the PIN, if present, using the MAC Generator Key and PIN Protect Key, respectively, from the same send session key set. The send session key set used is indicated by bit 53 (contains “1” or “2”) in each message. Session Keys must be statistically unique and replaced, at a minimum, once every hour or on every 256 Transactions, whichever occurs first.
| Node A | Node B | ||
| Send Session Keys Set 1 | Receive Session Keys Set 1 | ||
| MAC Key (KMACs1) | = | MAC Verification Key (KMACr1) | |
| PIN Protect Key (KPEs1) | = | PIN Protect Key (KPEr1) | |
| Send Session Keys Set 2 | Receive Session Keys Set 2 | ||
| MAC Key (KMACs2) | = | MAC Verification Key (KMACr2) | |
| PIN Protect Key (KPEs2) | = | PIN Protect Key (KPEr2) | |
| Receive Session Keys Set 1 | Send Session Keys Set 1 | ||
| MAC Verification Key (KMACr1) | = | MAC Key (KMACs1) | |
| PIN Protect Key (KPEr1) | = | PIN Protect Key (KPEs1) | |
| Receive Session Keys Set 2 | Send Session Keys Set 2 | ||
| MAC Verification Key (KMACr2) | = | MAC Key (KMACs2) | |
| PIN Protect Key (KPEr2) | = | PIN Protect Key (KPEs2) | |
When enciphered for transmission, each session key type will use a unique variant of the Key Enciphering Key in accordance with AS 2805 part 6.1 request response (logon) from the other before starting any other message exchange. When ready to logon, a party should attempt to logon and continue to attempt to logon until a successful response has been received. Upon receipt of an unsolicited logon (i.e. receiving a logon message when in an assumed logged on state) or a message with a response code indicating an irrecoverable error, a party should send an immediate logoff message and attempts to logon should be made as soon as possible. All logon response messages should be inspected to ensure that the response code indicates a successful logon
Changing Session keys
While one set of send session keys is being used, the other send session key set is randomly generated by the sending node and their KVCs generated, the keys are then enciphered under the Interchange Send KEK and transmitted to the receiving node in a 0820 Network Management Advice message.
When a 0820 message is received by the receiving node, the session keys are deciphered using the Interchange Receive KEK. These deciphered keys are set up as the set of receive keys specified by the set number contained in bit 53 of the 0820 message. The Key Verification Codes (KVCs) are calculated by the receiving node and transmitted to the sending node in bit 48 of the 0830 message.
When the 0830 Network Management Advice response message is received at the node initiating the key change, the KVCs contained in the 0830 message are validated. If the KVCs are correct, the new send session key set can be used immediately. If the KVCs are invalid, new send session key set must be generated and the whole process is repeated.
Sign off
Either node may terminate the transmission of financial messages by sending a Sign Off Advice. A Sign Off is accomplished by the transmission of a 0820 Network Management Advice Message with a NMIC (Bit 70) equal to ‘002’.
Key change during normal processing
A session key change can occur at any time; each node independently initiates the change of their send keys. The sender will advise their sending session keys to the receiver using a 0820 Network Management Advice message with a NMIC equal to ‘101’ indicating key change. Once a valid response (0830 message) is received and the KVCs confirmed, the new keys can be used.